0.Abstract
- 集成学习/神经网络模型笨重、计算耗费大、大量用户使用不便。
1.Introduction
1.1引入——类比昆虫
- 昆虫作为幼虫时擅于从环境中汲取能量,但是成长为成虫后确是擅于其他方面,比如迁徙和繁殖等。
- ML中,训练和测试两个阶段的目标不同:
- 对训练数据拟合得好、可以利用大量的计算资源、不需要实时响应、模型可以很大、易迁移
- 有很强的泛化能力、面临更加严格的要求包括计算资源限制、计算速度要求、易于部署
- 先训练复杂模型,再根据复杂模型训练简单模型“的效果要比直接训练简单模型的泛化效果要好。
1.2动机
- 一方面,在具有大量类别标签的训练任务中,一个复杂度很高的大模型地做法是为这些大量的标签分配概率分布。然而这种处理方式存在一个负作用:与正确标签相比,模型为所有的误标签都分配了很小的概率;然而实际上对于不同的错误标签,其被分配的概率仍然可能存在数个量级的悬殊差距。如:在识别一辆宝马汽车的图片时,分类器将该图片识别为垃圾车的概率是很小的,然而这种概率比起将其识别为胡萝卜的可能是会大出很多。然而由于在宏观上由于这些概率都很小,这一部分的知识很容易在训练过程中淹没。
- 另一方面,复杂的训练模型的训练过程中,所有的参数都经过了很强的正则化。通过这样的“蒸馏”方法,小模型的训练会模仿大模型的训练方式调整参数,效果要比从头开始训练的效果要好得多,因为小模型泛化能力更好。
1.3hard target与soft target
- 将大模型的泛化能力转移到一个小模型中的一个明显方法是利用大模型产生的类概率作为训练小模型的“软目标”。
- 可以使用相同的训练集或单独的训练集。
- 当软目标具有高熵时,它们比硬目标提供更多的信息,而且训练数据之间梯度变化更小。
- 小模型可以在更少数据上训练并且用更高学习率。
- hard target:比方说MNIST数据集是用来识别数字的,对于用来表示数字3的图片,它的label就是[0,0,1,0,0…0] ,从概率的角度上理解那就是说“图片显示的数字是3的概率是100%,是其他数字的概率是0%”,这就是所谓的hard target
- soft target:学习算法返回的可能就是[0.005 , 0.01 , 0.9 , … , 0.005]这样,代表“图片是1的概率是0.5%,图片是2的概率是1%,图片是3的概率是90%…”,这种非100%的结果就是所谓的soft target。(3更像2而1没这么像)。
1.4前人的研究
- Rich Caruana可以将集成的模型压缩到一个模型中,证明知识可以压缩,本文在此基础进一步研究。
- 由于软目标中概率都很接近于0,所以对交叉熵成本函数影响很小。
- 通过使用logits(softmax层的输入)来规避这个问题,用大模型的logits和小模型的logits均方误差来做损失函数。
1.4本文研究
- 由于软目标中概率都很接近于0,所以对交叉熵成本函数影响很小。
- 通过提高softmax的温度来规避这个问题,提高温度直到大模型产生了适当的软目标,然后使用同样的温度训练小模型。
- logits的使用其实是蒸馏的特殊情况。
- 训练集可以由未标记/原始训练集组成,使用原始训练集更好。特别是如果我们添加一个小的term,以鼓励小模型预测真实目标,以及匹配由大模型提供的软目标的目标函数。
2.蒸馏
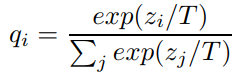
- 随着T的增大,最后softmax的输出qi会越来越“soft”,可以提供更大的信息熵,将已训练模型地知识更好地传递给新模型。T往常取1。
- 目的:用“蒸馏”把我们在应用端需要的配置的缩小模型从复杂模型中提取出来,使得小模型在预测实际目标的同时尽量匹配“软目标”。
- 步骤:
- 当transfer数据集标签未知:在transfer数据集上进行小模型训练,用每个数据在大模型中预测的软目标分布/T来训练,小模型训练也用相同的T,但训练后预测时,小模型使用T=1。
- 当transfer数据集标签已知:执行完上述步骤后,可以在小模型上单独使用已知标签,会有提升。由于由软目标产生的梯度的大小为1/t 2,因此在使用硬目标和软目标时,将T乘以2是很重要的。
- 使用正确标签修改soft target
- 对两个不同的目标函数使用加权平均,第1个目标函数权重小一些更好,这确保硬目标和软目标相对贡献大致不变。
- T=1的正确标签的交叉熵函数:使用小模型的logits
- 加T的软目标的交叉熵函数
-
损失函数:
-
正常:

- 每个transfer数据都贡献了一个交叉熵梯度dC/dzi
- zi是蒸馏后模型的logits。
- vi是复杂模型的logits。
- T很大,大于logits:近似计算

-
- logits的均值为0:

- T很大且logits均值为0时,等同于最小化 1/2(zi − vi)2。
- T很小时,logits被match的差一些,比平均值要负得多(At lower temperatures, distillation pays much less attention to matching logits that are much more negative than the average. )。
- 一方面,因为这些logits在大模型训练时完全不受损失函数的约束,所以可能噪音较多(This is potentially advantageous because these logits are almost completely unconstrained by the cost function used for training the cumbersome model so they could be very noisy. )。
- 另一方面,非常负的logits可以传达大模型中有用的信息(On the other hand, the very negative logits may convey useful information about the knowledge acquired by the cumbersome model. )
- 当蒸馏模型太小而无法捕获繁琐模型中的所有知识时,中间温度的工作效果最好,这强烈暗示忽略大负值的logits可能会有所帮助(We show that when the distilled model is much too small to capture all of the knowledege in the cumbersome model, intermediate temperatures work best which strongly suggests that ignoring the large negative logits can be helpful.)。
- 步骤:
- 第一步,提升大模型final softmax中的T,使得复杂模型产生一个合适的、适当柔软的“软目标” 。
- 第二步,采用同样的T来训练小模型,使得它产生相匹配的“软目标”。训练蒸馏模型时使用与大模型相同的T,但训练后小模型T为1。
3.MNIST实验
- 大模型:2层+1200整流线性单元+dropout+权重约束+输入数据任意方向抖动最多2像素:67错误
- 小模型:
- 2层+800整流线性单元+无正则:
- 温度为1:146错误
- 温度为20:74错误
- 2层+600整流线性单元+无正则:温度大于8较好
- 2层+60整流线性单元+无正则:温度在2.5~4较好
- 移除包含3得数据:见papper
- 2层+800整流线性单元+无正则:
4.语音识别实验
7.参考资料
- https://www.cnblogs.com/lainey/p/8531394.html
- http://blog.sina.com.cn/s/blog_76d02ce90102xnjf.html
- http://blog.csdn.net/cookie_234/article/details/72957100
- https://www.jianshu.com/p/4893122112fa
- https://zhuanlan.zhihu.com/p/24894102
- https://blog.csdn.net/zhongshaoyy/article/details/53582048
- https://www.zhihu.com/question/50519680