2.方法
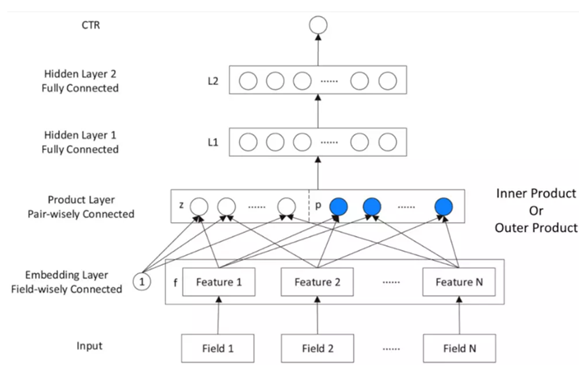
- Embedding层:
$z=(f_1,f_2,…,f_N),其中:f_i\in R^M为field_i取得的embedding,共有N个field$
$p={p_{i,j},其中i=1…N,j=1…N}=g(f_i,f_j),p\in R^{N*N}$
- Product层:拓展了神经网络的容量,增加了网络复杂度。
$l_z=(l_z^1,l_z^2,…,l_z^n,…,l_z^{D_1}),其中l_z^n=W_z^n\odot z$
$l_p=(l_p^1,l_p^2,…,l_p^n,…,l_p^{D_1}),其中l_p^n=W_p^n\odot p$
$其中A\odot B=\sum_{i,j}A_{i,j}B_{i,j},满足交换律$
- 隐藏层1:ReLU激活
- 隐藏层2:Sigmoid分类
2.1IPNN
- 定义$g(f_i,f_j)=<f_i,f_j>$
- layer1复杂度:
- 空间:$O(D_1N(M+N))$
- 时间:$O(N^2(D_1+M))$
-
复杂度优化:中间结果可以复用,假设$W_p^n=\theta ^n\theta^{nT}$(一阶分解,是个很强的假设),使得$W_p^n\odot p=\sum_{i=1}^N\sum_{j=1}^N \theta_i^n \theta_j^n<f_i,f_j>=<\sum_{i=1}^N \theta_i^nf_i,\sum_{i=1}^N \theta_i^nf_i>$
- 优化后的layer1复杂度:
- 空间:$O(D_1MN)$
- 时间:$O(D_1MN)$
2.2OPNN
- 定义$g(f_i,f_j)=f_if_j^T$
- layer1复杂度:
- 空间$O(D_1M^2N^2)$
- 时间$O(D_1M^2N^2)$
- 复杂度优化:
$p=\sum_{i=1}^N\sum_{j=1}^N f_if_j^T=f_{\sum}(f_{\sum})^T,f_{\sum}=\sum_{i=1}^N f_i$
- 优化后的layer1复杂度:
- 空间:$O(D_1M(M+N))$
- 时间:$O(D_1 M(M+N))$
2.3Discuss
- 加法交叉更像OR操作,乘法操作更像AND操作。
3.实验
3.1Datasets
- Criteo:1TB,7天训练,1天预测。以概率w下采样后有79.38M数据,1.64M特征。
- iPinYou:10天。7天训练,3天预测。19.50M数据、937.67K特征。
- 样本下采样后CTR的校准:$q=\frac{p}{p+\frac{1-p}{w}}$
3.2对比模型
- LR
- FM
- FNN
- CCPM
- IPNN
- OPNN
- PNN*:IPNN和OPNN结果concate到一起。
3.3其他配置
- sgd优化
- LR和FM用l2正则,FNN、PNN、CCPM用dropout(dropout率为0.5)
-
评估:AUC、RIG=1-Normalized Cross Entropy、Log Loss、RMSE,也用到了t检验
- 用长度为10的embedding。
- CCPM:1个embedding层、2个卷积层、max pooling、1个隐藏层。
- FNN:1个embedding层、3个隐藏层
- PNN:1个embedding层、1个product层、3个隐藏层。
3.4表现对比
- FM好于LR
- NN好于LR和FM
- PNN最好
- PNN*对于IPNN和OPNN没有特别好的提升
- 本文方法比LR和FM和其他DNN收敛更快。
3.5网络结构研究
- embedding长度:2、10、50、100。太长会导致dnn拟合能力差,容易过拟合。
- 网络深度:1、3、5、7。层数为3时较好。
- 激活函数:sigmoid、tanh、ReLU。tanh较好,ReLU也挺好。ReLU的梯度下降更快、稀疏激活(负值不会被激活)、无梯度消失问题。