Absract
- 特征工程困难、需要人工,有时需要穷举。
- DNN能自动学习特征交叉。但是其隐含地生成所有交互,并且不一定有效地学习所有类型的交叉特征。
- 本文:
- 引入了一种新颖的交叉网络(cross network),可以更有效地学习某些有界度的(bounded-degree)特征交互。
- DCN明确地在每一层应用特征交叉,不需要手动特征工程,并且为DNN模型增加了可忽略的额外复杂性。
- 我们的实验结果证明了其在CTR预测数据集和密集分类数据集上的最新算法在模型精度和内存使用方面的优越性。
1.Introduction
- 探索频繁的特征、交叉特征是做出良好预测的关键。然而web推荐系统数据大多数是离散的,导致对于特征探索有挑战性,这将大多数模型限制为线性模型,如LR。
- 线性模型简单、可解释、易拓展,但是表现力有限。且不支持交叉特征。需要特征工程。
- 本文提出的网络是cross网络与DNN共同训练的交叉网络。
- DNN捕捉特征之间的非常复杂的相互作用,但是与cross网络相比,其要更多的一个数量级的参数,无法明确形成交叉特征,可能无法有效学习特征交互。
- cross网络由多个层组成,最高程度的交互可由层深度确定,每个层基于现有层生成高阶交互,并保持与先前的交互。
1.1Related Work
- FM:将稀疏特征投射到低维稠密向量上,学习向量内积的特征交互。大量参数会产生不希望的计算成本。
- FFM:每个向量与field相关联。
- DNN+embedding:由于embedding和激活函数,DNN能学习到非平凡(non-trivial)的高阶特征交互。
- 残差网络使得可以训练非常深的网络。
- Deep Crossing:通过堆叠所有类型的输入(all types of inputs)来拓展残差网络并实现自动特征学习。
- Wide&Deep:将交叉特征作为线性模型的输入,将线性模型与DNN联合训练。其效果取决于正确选择交叉特征,这是一个指数复杂度的问题。
1.2Main Contributions
- 提出了DCN,支持稀疏和稠密输入,自动特征学习。有效捕获bounded degree的特征交互,学习高度非线性相互作用,计算成本低。
- 提出了新颖的cross网络,明确地用每层的特征交叉,有效地学习bounded degree的特征交互,不需要特征工程。
- 网络简单有效。每层最高多项式degree(the highest polynomial degree)在每层增加,degree最终由层数决定。网络由degree的所有交叉项组成,直到最高层,每层系数都不同。
- 内存使用效率高,易于实现。
- 实验结果表明:DCN的logloss比DNN更低,参数数量少了接近一个数量级。
2.DCN
2.1embedding与stacking层
- 输入:连续值、离散值。
- 将连续值和离散值的embedding给stack起来:

2.2.Cross网络
- 交叉网络的核心思想是以有效的方式应用显式特征交叉。交叉网络由交叉层组成,每个层具有以下公式:

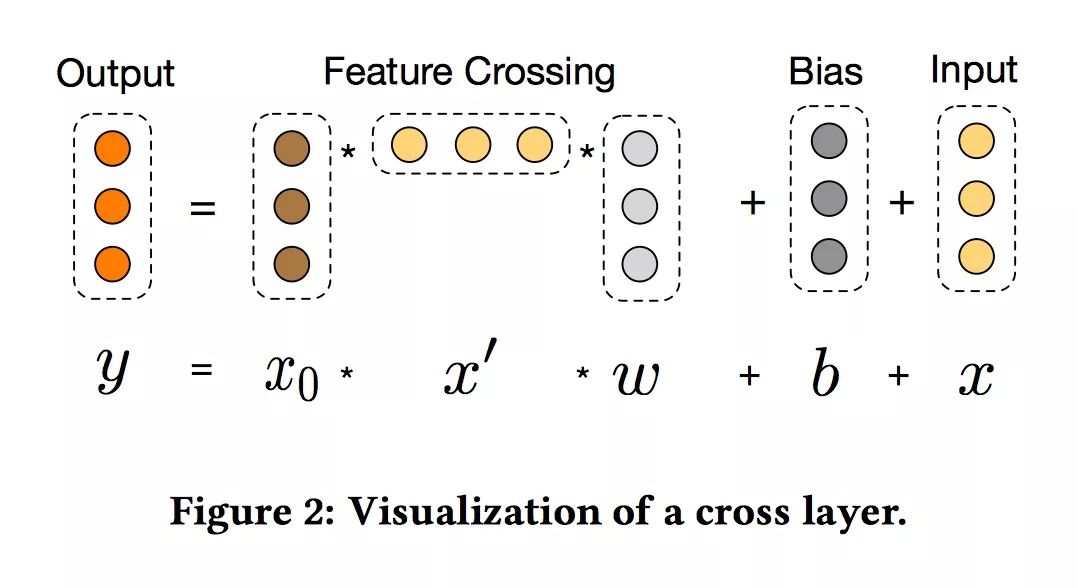
- 特征高维交叉:交叉网络的特殊结构使交叉特征的程度随着层深度的增加而增大。
- 参数量:
- 如果用Lc表示交叉层数,d表示输入维度。参数的数量参与跨网络参数为:d * Lc * 2 (w和b)。
- cross网络的时间和空间复杂度在输入维度上是线性的。 因此,与dnn相比,cross网络引入的复杂性可忽略不计,使DCN的总体复杂性保持在与传统DNN相同的水平。
- This efficiency benefits from the rank-one property of x0xTl ,which enables us to generate all cross terms without computing or storing the entire matrix.
- cross网络的参数少限制了模型容量。为了捕捉高阶非线性的相互作用,模型并行地引入了一个深度网络。
2.3Deep网络
- Ld:神经网络层数
- m:神经元数
- 参数量: d×m+m+(m +m)×(Ld−1) 。
2.4Combination层
- 将Deep网络和Cross网络的输出给concate起来,然后送入标准logits层(就是一个全连接层)。
- 公式:

2.5网络结构

2.6损失函数
- 加了正则项的logloss

3.Cross网络分析
- 假设bi=0
-
令第j层元素的权重为w_j^{i},对于多下标(multi-index):α=[α1,⋅⋅⋅,αd]∈N^d,x=[x1,…,xd]∈Rd,定义 α =∑_i=1^{d}αi。将xα11xα22⋅⋅⋅xαdd交叉项定义为 α ,多项式定义为它的高阶项。
3.1多项式近似
-
由weierstrass逼近定理,平滑假设下任何函数的任何精度都可以通过多项式逼近。
-
我们从相同degree的多项式角度分析Cross网络。Cross网络是一种高效、富有表现力的方式,是比相同degree的多项式类更好地概括为真实世界数据集的方式。
-
用Pn(x)表示n度的多元多项式,如下:

-
每个多项式在这类上都有O(dn)的参数、交叉网络包含所有的交叉项发生在多项式相同的程度,每一项的系数彼此不同。
-
定理:一个l层交叉网络,i+1层可以定义为xi+1=x0xTiwi+xi。网络的输入为:x0=[x1,x2,⋯,xd]T,输出为:gl(x0)=xlTwl。那么多元多项式gl(x0)产生以下情形:

3.2FM的泛化
- Cross网络利用了FM的参数共享思想,并进一步拓展到更深层的结构。
- 在DCN中,xi与{w_k^{i}}{k=0}^l有关,xixj的权重是{w_k^{i}}{k=0}^l、{w_k^{j}}_{k=0}^l。
- 两个模型都具有独立于其他特征的每个特征学习的一些参数,并且交叉项的权重是相应参数的特定组合。
- 参数共享不仅使模型更有效,而且使模型能够推广到看不见的特征交互,并且对噪声更具鲁棒性。
- FM是隐层结构且是degree2以内,DCNdegree是无限的,将单层拓展到多层和高度交叉。
- 与高阶FM不同,DCN的参数量只随输入维数线性增长。
3.3有效的映射
-
每个cross layer以有效的方式将x0和xl之间的所有的成对交叉(pairwise interaction)退回到输入的维度。
-
如果将cross layer的输入x构建pairwise interaction为xixj,然后映射回d维,最简单的方法也是n3的复杂度。
-
cross layer是这么做的 :x’=xixjw,这就等价于:
4.实验结果
4.1Criteo Display Ads Data
- 预测CTR,有13个整数特征、26个类别特征。
- logloss的0.0001的改进被认为是显著的。
- 包括7天共11G用户日志,4100万条记录。
- 使用前6天训练,第7天一半验证一半测试。
4.2实现细节
- tf实现
- 预处理:实值特征被标准化+log变换,离散特征embedding为6*(category cardinality)^(1/4)维向量,所有embedding向量concate起来后是1026维。
- 算法优化:adam+mini batch size-512+batch normalization
- 正则:用early stop,L2和sropout没啥提升。
- 超参数:
- 网格搜索
- dnn:隐藏层层数2-5,每层神经元个数32-1024。
- cross layer:1-6。
- 初始学习率从0.0001到0.001,增量为0.0001。
- epoch最多150000,超过该步骤过拟合(由early stop得出)。
4.3模型对比
- DNN:嵌入层,输出层和超级参数调整过程与DCN相同。
- LR:使用Sibyl实现分布式LR。连续值离散化处理(log离散)。通过特征选择工具选择交叉特征。
- FM:
- Wide&Deep:wide组件输入原始稀疏特征,依赖于穷举搜索和领域知识来构造交叉特征。
- Deep Crossing:与DCN相比,DC不形成明确的交叉特征,主要依靠堆叠和残差模块来建立隐式交叉。我用相同的embedding layer加relu层,以生成一系列残差单元的输入。残差单元的数量1-5,输入尺寸和cross尺寸从100-1026。
4.4模型表现
- 最佳参数:
- DCN:dnn网络2层,每层1024神经元。6个cross层。
- DNN:5层,每层1024个神经元。
- DC:5个残差单元,输入424维, cross 537维。
- LR:交叉特征42个。
- 表1:最深的DCN网络表现最好,仅仅使用了最优DNN网络的40%的内存。logloss的平均值、标准差而言,DCN始终优于其他模型。
- 表2、表3:Cross网络仅引入O(d)额外参数。由于交叉网络能够更有效地学习有界度特征交互,因此DCN比单个DNN的存储效率高出近一个数量级。在小参数量网络中,交叉网络中的参数数量与深度网络中的参数数量相当,并且明显的改进表明交叉网络在学习有效特征交互方面更有效。 在大参数量网络中,DNN弥补了一些差距; 然而,DCN仍然大大超过DNN,这表明它可以有效地学习某些类型的有意义的特征交互,即使是巨大的DNN模型也不能。
- 表4:我们首先在相同层数和层大小的情况下将DNN的最佳性能与DCN的性能进行比较,然后针对每个设置,我们展示了在添加更多交叉层时验证对数损失如何变化。在相同的实验设置下,来自DCN模型的最佳logloss始终优于来自相同结构的单个DNN模型的logloss。 所有超参数的改进是一致的,这减轻了初始化和随机优化的随机效应。
- 图3:显示随着cross layer的增加,logloss的变化。当向模型添加1个交叉层时,有明显的改进。 随着更多的交叉层被引入,对于某些设置,对数损失继续减少,表明引入的交叉项在预测中是有效的; 而对于其他人来说,logloss开始波动甚至略微增加,这表明引入的更高程度的特征交互没有帮助。
4.5非CTR数据
- DCN在非CTR预测问题上表现良好。
- 数据集:forest covertype(581012样本,特征)、Higgs(11M样本,28个特征)。
- 划分:训练集验证集90%+10%
- 超参数调优:网格搜索。dnn层数1-10,神经元个数50-300,cross层层数4-10,残差单元数目1-5(输入维度、cross维度50-300)。
- forest covertype数据结果:最佳测试精度0.9740,内存消耗最小,DNN、DC均是0.9737。最佳超参数:尺寸为54的6个cross层和6个尺寸为292的DCN的deep层,7个针对DNN的尺寸为292的deep层,以及具有输入尺寸271和针对DC的交叉尺寸287的4个残差单元。
- Higgs:最佳测试logloss 0.4494,内存消耗是DNN的一半,DNN是0.4506。最佳超参数:4个尺寸为28的cross层,4个用于DCN的尺寸为209的deep层,用于DNN的10个尺寸为196的deep层。
5 CONCLUSION AND FUTURE DIRECTIONS
- DNN在自动特征学习中很受欢迎;然而,所学习的特征是隐含的和高度非线性的,并且网络可能不必要地大而且在学习某些特征方面效率低。
- 本文提出的深度与交叉网络可以处理大量稀疏和密集的特征,并与传统的深度表示一起学习有界度的(bounded degree)显式交叉特征。每个交叉层的交叉特征程度增加1。在模型精度和内存使用方面,我们的实验结果证明了它在稀疏和密集数据集上优于现有算法的优越性。
