Absract
- 在本文中,我们建立了FFM作为一种有效的方法来分类大型稀疏数据,包括来自CTR预测的数据。
- 首先,我们提出了有效的FFM训练方法。 然后我们全面分析FFM并将此方法与竞争模型(competing models)进行比较。 实验表明,FFM对于某些分类问题非常有用。 最后,我们发布了一套供公众使用的FFM。
1.Introduction
- 如论文例子所示,关联特征对CTR预测至关重要,然而线性模型难以学习这些信息。
- 基于FM的PITF方法被提出来用于个性化标签推荐。在2012年KDD杯中,PITF的轮廓(被称为“因子模型”)由“Team Opera Solutions”提出。 由于该术语过于笼统并且很容易与因子机混淆,因此本文将其称为“场感知因子机”(FFM)。
- PITF考虑三个特殊字段:user、item、tag,FFM更加通用。PITF中有以下几个结论:
- 用SGD来优化,为避免过拟合,之训练一个epoch
- FFM在他们尝试的六种模型中最好。
- 本文成果
- 将FFM与Poly2和FM进行比较,首先进行概念性的比较,再做实验查看准确性和训练时间的差异。
- 提出了训练FFM的计数,用于FFM的有效并行化算法以及使用early stop来避免过拟合。
- 发布了一个开源软件。
2. POLY2 AND FM
-
POLY2:d=2的多项式映射通常可以有效地捕获特征组合连接信息。通过在d=2的显式映射上使用线性模型,训练和测试时间都比用核方法快得多。poly2模型会为每一个特征对学习一个权重:
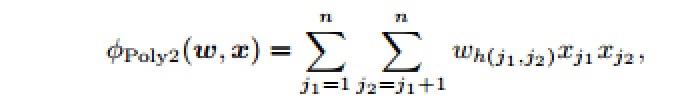
- h(j1,j2)是一个把j1和j2编码成一个自然数的函数
- 公式的计算复杂度是O(n^2),n表示每个样本的非0数目的平均。
-
FM:FMs是为每个特征学习一个隐向量表示,每个隐向量包含k维,这样特征交互的影响就被建模成2个隐向量之间的内积:
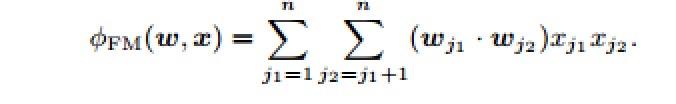
- 通过一些计算技巧可以把计算复杂度降到O(nk)
-
在稀疏数据集上,FMs模型要比poly2模型好一些,比如对于论文的例子,对于pair(ESPN,Adidas)只有一个唯一的负样本,通过poly2模型会学习到一个大的负向权重对于这个pair,然而对于FMs来说,因为它是学习ESPN和Adidas的隐向量表示,所有包含ESPN的样本和所有Adidas的样本都会被分别用来学习这2个隐向量,所以它的预测会更准确一些。
3.FFM
3.1模型
-
FFM的想法源于PITF[7],PITF用于具有个性化标签的推荐系统。 在PITF中,它们假定三个可用字段,包括user,item和tag,以及在单独的隐空间中分解(user,item),(user,tag)和(item,tag)。 在[8]中,他们将PITF推广到更多字段(例如,AdID,AdvertiserID,UserID,QueryID),并将其有效地应用于CTR预测。 因为[7]的目标是推荐系统,并且仅限于三个特定域(user,item和tag),[8]缺乏关于FFM的详细讨论,在本节中我们提供了关于CTR预测的FFM的更全面的研究。 对于大多数CTR来说,特征可以被group为field。 在上述例子中ESPN,Vogue,NBC可以被group成Publisher,而Nike,Gucci,Adidas属于Advertiser,FFM会充分利用group的信息。
-
FM中每个特征只有一个隐向量表示,这个隐向量被用来学习与其他任何特征之间的影响。 考虑ESPN,w(ESPN)被用来学习与Nike的隐性影响w(ESPN)w(Nike),还被用来学习与Male的影响w(ESPN)w(Male),然而由于Nike和Male属于不同的域,它们的隐性影响是不一样的。
-
FFM模型认为vi不仅跟xi有关系,还跟xj所属的Field有关系,即vi成了一个二维向量vF×K,F是Field的总个数。
-
在FFMs里面,每个特征会有几个不同的隐向量,上述例子的FFMs表示如下:

-
我们看到,为了学习(ESPN,NIKE)的潜在影响,使用wESPN,A是因为Nike属于广告商场。使用了wNike,P是因为ESPN属于字段Publisher。
再次,为了学习(EPSN,男性)的潜在影响,使用WESPN; G是因为男性属于性别领域,而wMale; P被使用是因为ESPN属于字段Publisher。在数学上,
-
公式:
- f1、f2:是j1和j2的域
- f:域的数目
- nfk:FFM的变量数
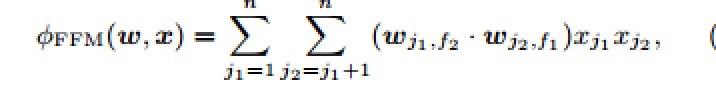
- 上式可以在线性时间O(非n^2k)内计算。由于FFM中每个隐变量通常只需要通过特定域来学习,通常有:kFFM«kFM
3.2目标函数
- 除了φLM(w; x)被φFFM(w; x)替换之外,该优化问题与LR相同。
3.3参数估计
-
使用随机梯度法SGD的升级版AdaGrad。
- 因为x非常稀疏,所以只更新具有非零值的维度。
- 使用AdaGrad [10],因为[12]已经证明了矩阵分解的有效性,矩阵分解是FFM的一个特例。
- 算法描述:
- η:学习率
- w:初始化从均匀分布[0,1/根号k]中取样
- G:




-
将每个样本标准化以具有单位长度使得测试精度稍微更好并且对参数不敏感。
-
最近还提出了一些自适应学习速率调节表,如[10,11]所示,以促进SGD的训练过程。
-
并行化:用Hogwild [13],它允许每个线程独立运行而不需要任何锁。
-
输入数据加入域信息:基于libsvm数据结构,为每个特征标明属于那个域。
- 离散特征:通常转换为onehot特征,离散特征只保存为1的那个特征,其余为0的不存。
- 数值型特征:离散化,flota转为int,取整。
- 所有特征属于同一个域:通常出现在NLP问题中,转换为FM问题。
4.实验
- FFM对epoch是敏感的。
4.1实验settings
- 数据集:Criteo、Avazu(Kaggle比赛)
- 特征工程:用夺冠solution,但是不用夺冠solution的复杂组件(components),如模型融合。
- 数据划分:test集的数据不公开,分为A、B榜(score公开/不公开),抛弃。把其余数据split出来10%+作为验证数据。
- 实验平台:
- 实现:LM、POLY2、FM、FFM in C++。
- 对于FM、FFM,用SSE指令提升内积运算效率。
- 用OpenMP实现并行化。
- 代码拓展性:无论使用何种模型,都会存储字段信息。
4.2超参数
- k、λ、η :见论文中图。
- k:对logloss几乎无影响
- λ:太大模型表现不好,小的会更好,但会过拟合。
- η:小的收敛慢,但是表现好。
4.3Early Stopping
- 避免过拟合:每个epoch后看验证集loss,若loss涨了就stop training
- 避免在验证集上表现好,在训练集上表现差:lazy update、ALS-based优化方法。
4.4并行化
- 线程数少加速较好,若使用太多线程,加速不会太大改善。因为如果两个或多个线程尝试访问相同内存地址,则就会冲突、等待。
4.5实验结论
- LibLINEAR:l2惩罚,两种优化方法:牛顿法、坐标下降法。
- LibLINEAR-Hash:LibLINEAR现有的poly2拓展不支持散列,因此做了适当修改。
- LIBFM:三种优化方法:SGD、交替最小二乘、MCMC。交替最小二乘效果最好。我们自己实现的FM比LIBFM更快,原因:LINBFM的交替最小二乘更复杂,我们用SGD+SSE。
- FFM在对数损失函数下,优于其他模型,但是训练时间比LR、FM更长。POLY2是所有模型中最慢的。
- LR是凸优化问题,对于LR和POLY2,SGD牛顿法、坐标下降法应该取得相同结果。但是结果却不是这样,SGD实现的LR比LIBLINEAR表现更好。这说明:即使问题是凸的,优化方法的停止条件也会影响结果模型的性能。
4.6非CTR数据集
- 当数据集仅包含数字特征时,FFM可能没有明显的优势。
- 用dummy的话,FFM不会比FM好。
- 用离散化的话,FFM虽然是最好的,但是性能差。
- 当不够稀疏时,FFM可能没有明显优势。
5.结论
- FM在logloss损失下优于LR、POLY2、FM,但是训练时间更长。
- 未来:其他优化方法在FFM上应用,调参。
参考资料
- 论文
- https://blog.csdn.net/jediael_lu/article/details/77772565