Absract
- 本文介绍了因子机,它结合了SVM和因子分解模型(factorization models)的优点。
- FM用实值向量,与SVM相比FM使用因子分解参数(factorized parameters)模拟所有特征相互作用。因此,即使在SVM不适用的具有巨大稀疏特征(如推荐系统)问题中,他们也能够估计特征的相互作用。
- FM的模型方程可以在线性时间内计算,FM可以直接优化。因此,与非线性SVM不同,对偶形式的转换不是必需的,并且可以直接估计模型参数,而无需样本中的任何支持向量。 我们展示了FM与SVM的关系以及FM在稀疏数据中进行参数估计的优势。
- 有很多不同的因子分解模型(如矩阵分解、并行因子分析、SVD++、PITF、FPMC)。这些模型的缺点是它们不适用于一般预测任务,仅适用于特殊输入数据。 此外,他们的模型方程和优化算法是针对每个任务单独导出的。 我们通过指定输入数据(即特征向量)表明FM可以模仿这些模型。 这使得即使对于没有分解模型专业知识的用户,FM也很容易适用。
1.Introduction
- 在协同过滤等算法中,SVM不大行,最好的模型是标准矩阵/张量因子分解模型的直接应用。
- 本文表明SVM在这些任务中不成功的唯一原因是它们无法在非常稀疏的数据下学习复杂的非线性内核空间中的参数。
- 张量因子分解模型的缺点是:不适用于标准预测数据(如实值特征向量)、需要对不同的任务单独生成不同的专用模型
- 本文引入FM,是通用分类器。
- 能在非常高的稀疏度下估计参数。与SVM中的多项式内核相比,FM模拟所有变量交互,但使用分解参数化(factorized parametrization)而不是像SVM中那样的密集参数化(dense parametrization)。
- FM的模型方程可以在线性时间内计算,它仅取决于线性数量的参数。 这允许直接优化和存储模型参数,而无需存储任何训练数据(例如,支持向量)。 与此相反,非线性SVM通常以对偶形式进行优化,并且计算的模型方程取决于部分训练数据(支持向量)。
- FM是一种可以与任何实值特征向量一起使用的通用预测器。 与此相反,其他最先进的因子分解模型仅适用于非常有限的输入数据。
2. PREDICTION UNDER SPARSITY
- 机器学习常见任务:
- 分类:hinge损失或logit损失
- 回归:最小二乘误差
- 排序:训练一个分值,再按分值排序,分值由成对训练数据(两者之间有先后关系)学习得到。
- 在本文中,我们处理x高度稀疏的问题,即几乎矢量x的所有元素xi都为零。
- 令m(x)为特征向量x中的非零元素的数量,非mD为所有向量x∈D的非零元素数m(x)的平均数。巨大稀疏性的一个原因是底层问题涉及大的类别变量域( One reason for huge sparsity is that the underlying problem deals with large categorical variable domains.)。
- 例子:用户给电影评分(见论文)。
3.d=2(二阶交互)的FM
3.1模型
-
众所周知,对于任何正定矩阵W,一定存在矩阵V,使得W = V·Vt,条件是k足够大。 这表明如果k被选择得足够大,则FM可以表达任何交互矩阵W。然而,在稀疏数据中,通常应该选择小的k,因为没有足够的数据来估计复杂的相互作用W。限制k(FM的表达性)导致更好的泛化,从而改善稀疏性下的交互矩阵。
-
公式:
- V中的vi是具有k个因子的第i个变量,k是定义了分解的维数的超参数。
- n:特征维度
- w0:全局偏置。
- wi:第i个变量的强度
- wi,j:=<vi,vj>:第i和第j个变量之间的相互作用。不使用简单的参数wi,j∈R进行每次交互,而是通过向量v对其进行分解来交互。这是高稀疏下进行参数估计的关键。
- FM通过因式分解打破了交互参数(wij)的独立性。
- O(kn2)的复杂度,因为必须计算所有成对相互作用

- 上式可以再线性时间O(kn)内计算。
- 由于成对相互作用的因子分解,没有直接依赖于两个变量的模型参数(例如具有索引(i,j)的参数)。
- 此外,在稀疏性下,x中的大多数元素是0(即m(x)很小),因此,仅需要在非零元素上计算和。
- 因此,在稀疏应用中,分解机器的计算是O(k非mD)
- 证明:
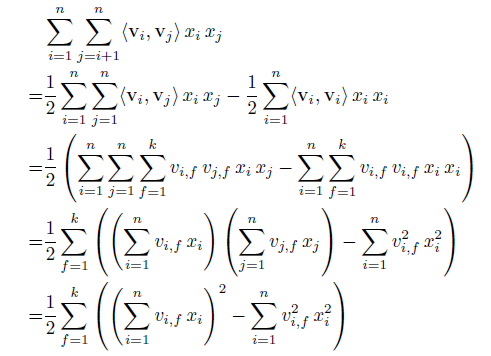
- 原理:
- 在稀疏数据中,通常没有足够的数据来直接和独立地估计变量之间的交互参数。因子机通过分解交互参数来破坏交互参数的独立性。通常,这意味着一个交互的数据也有助于估计相关交互的参数。
- 以上述电影为例,我们要估计用户A和电影ST的关系w(A&ST)以更好地预测y,如果是简单地考虑特征之间的共现情况来估计w(A&ST),从已有的训练样本来看,这两者并没有共现,因此学习出来的w(A&ST)=0。而实际上,A和ST应该是存在某种联系的,从用户角度来看,A和B都看过SW,而B还看过ST,说明A也可能喜欢ST,说明A很有可能也喜欢ST。而通过向量v来表示用户和电影,任意两两之间的交互都会影响v的更新,从前面举的例子就可以看过,A和B看过SW,这样的交互关系就会导致v(ST)的学习更新,因此通过向量v的学习方式能够更好的挖掘特征间的相互关系,尤其在稀疏条件下。
3.2损失函数
- 平方误差
- logits损失
- hinge损失
3.3参数估计
- 通过SGD梯度下降学习,计算如下:
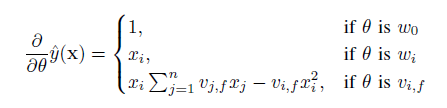
- Σj=1,n,vj,fxj这部分求和跟样本i是独立的,因此可以预先计算好。
- 每个梯度都是O(1)复杂度,……
4.多阶交互的FM
- 公式:

- 复杂度:看起来复杂度高,但是其实可以在线性时间完成
5.优点
- 即使在高稀疏度下,也可以估计值之间的相互作用。 特别是,可以概括为未观察到的相互作用。
- 参数的数量以及预测和学习的时间是线性的。 这使得使用SGD的直接优化成为可能,并且允许针对各种损失函数进行优化。
6.FM vs SVM
-
线性核SVM对应于FM的一阶形式(d=1):
- 线性核为K(x,z)=1+<x,z>
-
多项式核SVM对应于FM的高阶形式:
-
多项式核为K(1+<x,z>)^d
-
多项式核映射后的模型函数表示为:多项式核映射后的模型函数表示为:
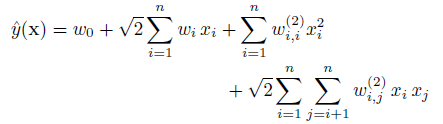
-
当d=2时为二次多项式,表示为:
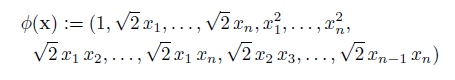
-
-
区别:
- SVM的二元特征交叉参数是独立的,而FM的二元特征交叉参数是两个k维的向量vi、vj,这样子的话,<vi,vj>和<vi,vk>就不是独立的,而是相互影响的。
- 线性svm只有一维特征,在稀疏的数据中能学习好参数(由于模型简单),但不能挖掘深层次的组合特征,在实际预测中并没有很好的表现;
- 多项式svm正如前面提到的,交叉的多个特征需要在训练集上共现才能被学习到,否则该对应的参数就为0,这样对于测试集上的case而言这样的特征就失去了意义,因此在稀疏条件下,SVM表现并不能让人满意。而FM不一样,通过向量化的交叉,可以学习到不同特征之间的交互,进行提取到更深层次的抽象意义。
- FM可以在原始形式下进行优化学习,而基于kernel的非线性SVM通常需要在对偶形式下进行
- FM的模型预测是与训练样本独立,而SVM则与部分训练样本有关,即支持向量。
7.FM vs 其他
- 用于类别变量:MF, PARAFAC
- 用于特定数据和任务:svd++、pitf、fpmc
- FM可以模拟以上模型
7.1矩阵和张量分解
- 矩阵分解(MF)分解了离散特征U和I的关系。使用此特征向量x的FM与矩阵分解模型相同。
- 对于两个以上类别变量作为输入的预测问题,fm包括一个嵌套的并行因子分析模型(parafac)。
7.2SVD++
- 对于回归、预测任务,矩阵分解模型被改进为SVD++模型。FM可以使用一下输入数据来模拟此模型: